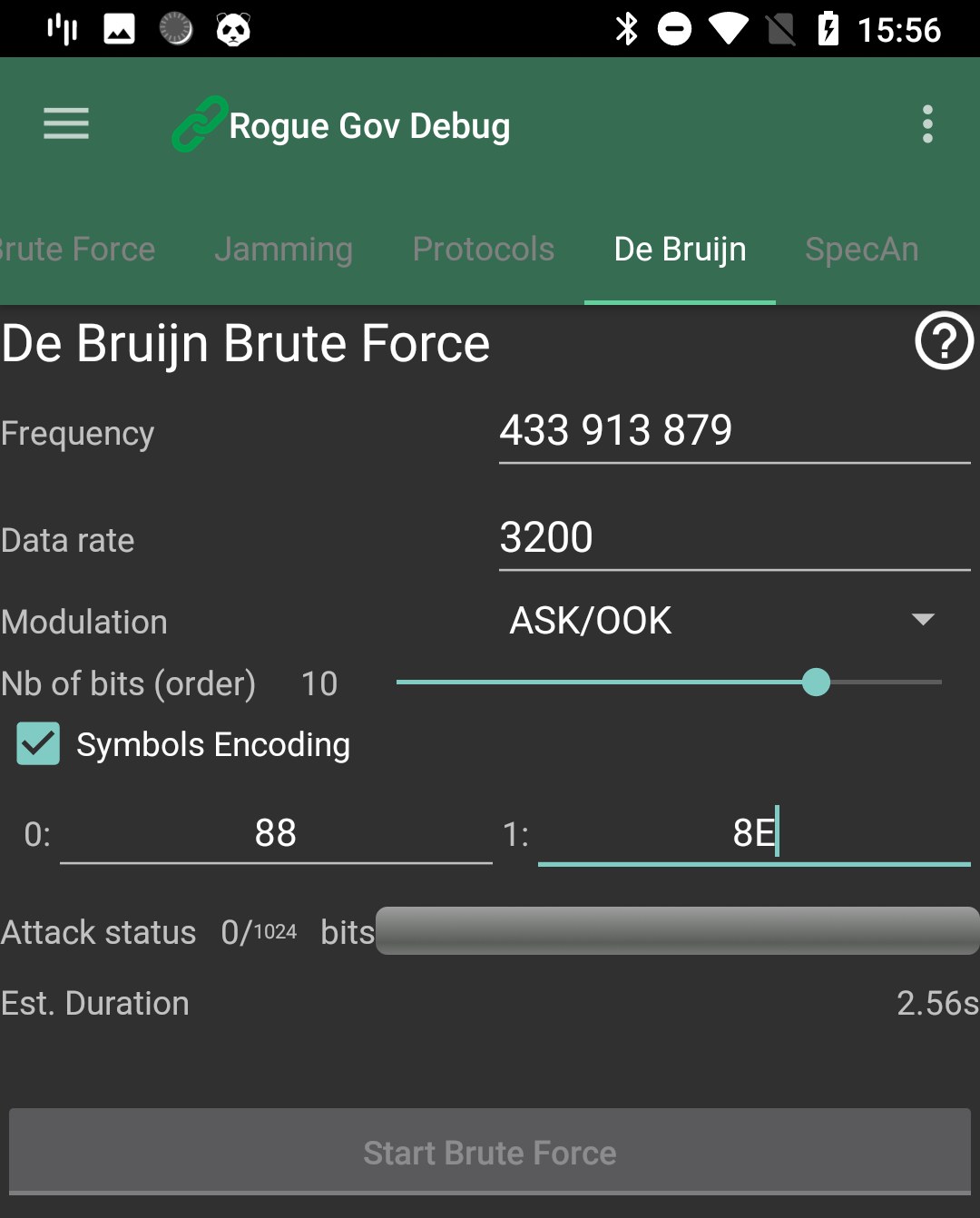
Starting from PandwaRF Android App v1.7.0 (Nordic release 0.12.0), PandwaRF Rogue now supports an Enhanced De Bruijn Brute Force.
This new De Bruijn Brute Force attack method allows converting a binary symbol (0/1) into a byte instead of a bit, giving more flexibility in the De Bruijn sequence generated by Rogue.
In this post, you will find more details on how this new Enhanced De Bruijn attack works related to the normal De Bruijn attack.
De Bruijn Brute Force
The De Bruijn sequence is an algorithm used to efficiently produce every possible code in as few bits as possible. It is very effective against old receivers that contain shift registers. Using the De Bruijn mathematical algorithm, PandwaRF Rogue Gov is able to brute force a 12 bit code in 1.2 s instead of a normal brute forced duration of 8mn.
Besides classical RF parameters such as frequency, data rate and modulation, the only parameter needed is the length of the codeword to Brute force.
Old receivers usually use from 8 bit to 12 bit codewords.
Note on De Bruijn attack: this attack only works on some old receivers.
Symbol encoding
The De Bruijn Brute Force can also be made using Symbols Encoding. While normal De Bruijn brute force is made using binary symbols, using Symbol Encoding allows the translation of symbols onto a byte instead of a bit.
Bit encoding (normal De Bruijn)
If bit encoding is used, one De Bruijn symbol is converted into one bit and user cannot change the mapping.
- symbol 0 => bit ‘0’
- symbol 1 => bit ‘1’
The duration of a symbol is the same as the duration of one bit (1/3200 bits/s = 312 µs).
For an order of 10 (codeword of 10 bits) the length of the complete De Bruijn sequence is 210 + (10 -1) = 1033 symbols.
As each symbol is also a bit, the sequence is 1033 bits long, which is 322 ms (1033 * 312 µs).
Symbol encoding (enhanced De Bruijn)
If byte encoding is used, one De Bruijn symbol is converted into eight (8) bits and user can change the mapping.
Ex:
- symbol 0 => bit ‘0x88’
- symbol 1 => bit ‘0x8E’
As each symbol is converted to a byte, the sequence of 1033 symbols become 1033 * 8 bits, which is 2.5 s (322 ms * 8).
Note that the duration of a symbol is 8 times the duration of one bit (8 * 1/3200 bits/s = 2.5 ms).
Comparison – normal De Bruijn vs enhanced De Bruijn
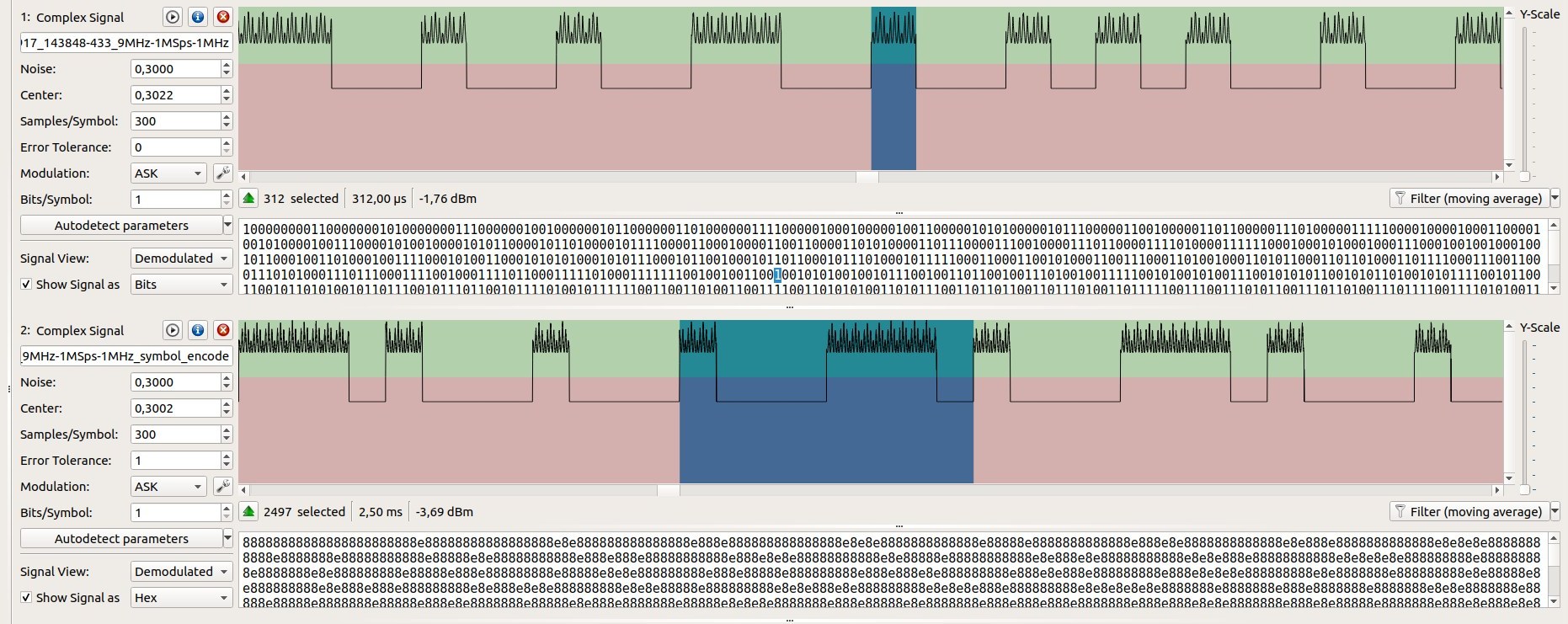
Figure 1 Duration of De Bruijn symbol. Bit encoding (top) vs symbol encoding (bottom)
Figure 2 shows the duration of the Full De Bruijn sequence in the 2 cases (bit encoding vs symbol encoding).
- On the top part, the normal De Bruijn sequence has a duration of 314 ms (vs 322 ms theory)
- On the bottom part, the Symbol encoded De Bruijn sequence has a duration of 2.33 s (vs 2.5 s theory)
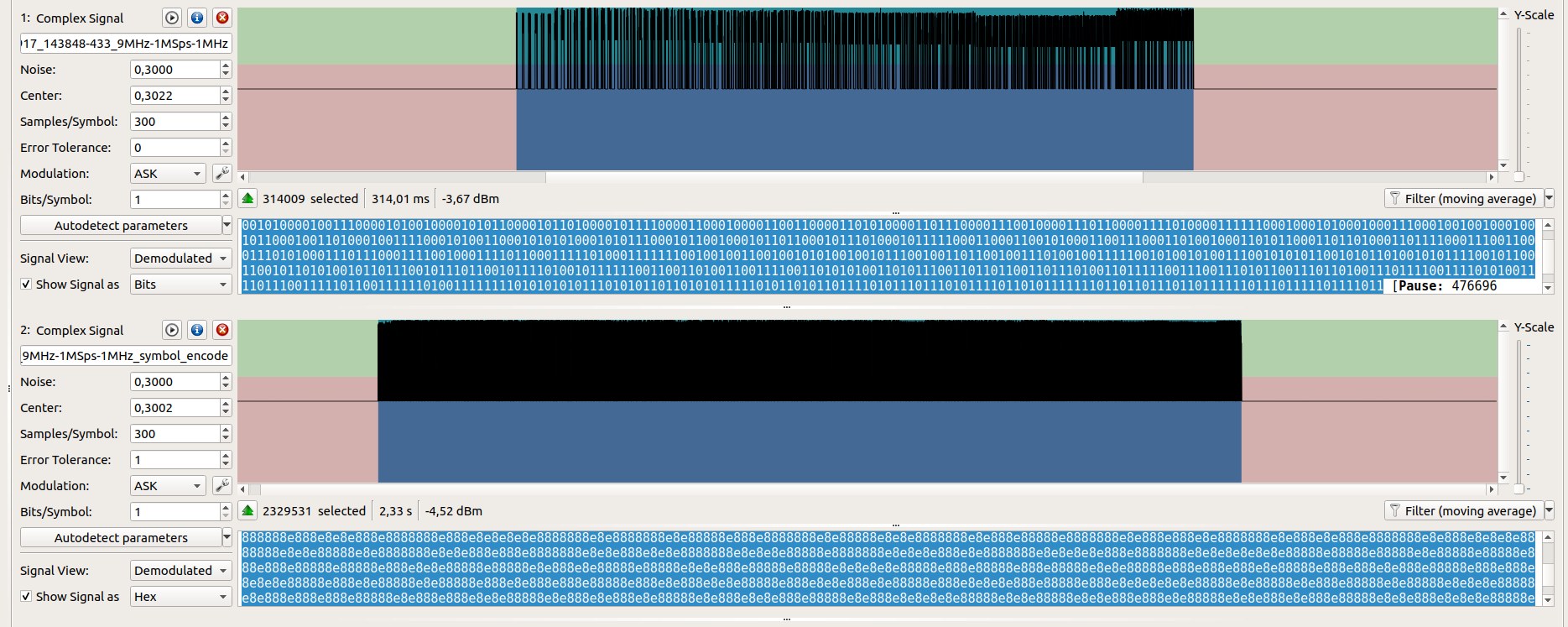
Figure 2 Duration of De Bruijn sequence. Bit encoding (top) vs symbol encoding (bottom)
Figure 3 shows the content of the De Bruijn sequence in both encodings:
- Bit encoding: the sequence contains only 0/1 bits
- Symbol encoding: the sequence contains only 0x88/0x8E bytes (b10001000/b10001110) bits.
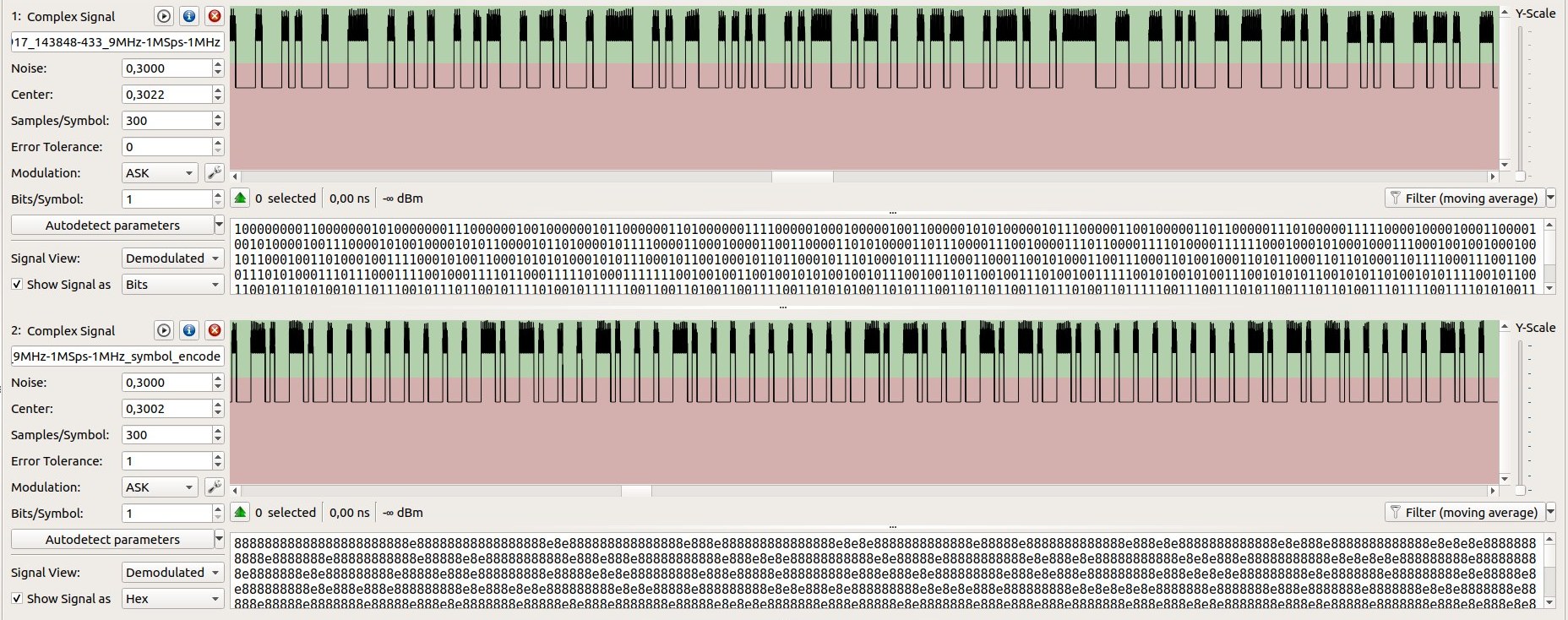
Figure 3 Inside a De Bruijn sequence. Bit encoding (top) vs symbol encoding (bottom)
Of course in the example above, encoding onto bytes ‘88’ and ‘8E’ is arbitrary and can be changed by user.
For more information about the De Bruijn attack and vulnerable devices, refer to http://samy.pl/opensesame/
Check also this De Bruijn Sequence Generator for Faster Shift Register Code Bruteforcing.